THE DETECTION OF GRAVITATIONAL RADIATION
On September 14, 2015 the gravitational wave detectors of the LIGO/VIRGO collaboration observed the signal of a coalescence of two black holes with masses 36 and 29 solar masses at a distance of about 1.3 billions of light-years. This extraordinary discovery opens up the way to gravitational wave astronomy. A huge step forward in astrophysics as well as fundamental physics is expected in the coming years. Physicists at the Institut d’Astrophysique de Paris have pioneered the development of new methods that permit to obtain, from the theory of general relativity, a very precise and reliable prediction for the gravitational waveform generated by the coalescence of neutron stars or black holes. These methods are based on analytic approximations in general relativity, and notably on the so-called "post-Newtonian" expansion. The post-Newtonian gravitational wave templates play a crucial role in the process of detection and signal analysis in gravitational wave detectors. The post-Newtonian waveform is valid in the initial inspiraling phase of the coalescence and is then matched to purely numerical calculations of the final merger of the black holes.
A major discovery
Gravitational waves are ripples of space-time predicted very early on by the theory of general relativity (see Figure 1). They propagate at the speed of light and are generated by extremely rapid (i.e. "relativistic") displacements of large amounts of matter.
The properties of gravitational waves are very different from those of electromagnetic waves. Produced by the bulk motion of large masses (contrary to light waves, which are generally made of the incoherent superposition of many emissions from the individual atoms that make-up the source), they can be viewed as a sort of analogue of sound waves. In addition, they interact extremely weakly with matter, so that they can travel nearly unattenuated on very large distances. Gravitational wave astronomy, which is now starting with this discovery, will be complementary to traditional astronomy based on electromagnetic radiation (in all its frequency bands, radio, visible, X, etc.). It will allow researchers to study violent phenomena that are in general invisible in electromagnetic radiation and occur at very large distances in the Universe.
On September 14, 2015, at exactly 9 hours 50 minutes and 45 seconds in universal time, the LIG0 (Laser Interferometric Gravitational Observatory) detector located on the American gulf coast in the state of Louisiana, observed a gravitational wave which had been emitted in the last instants of a system of two black holes[1], when the two black holes collided and merged. This event has been designated as "GW150914" (GW for gravitational wave, followed by the date) and occurred about 1.3 billion years ago. Since then, the gravitational wave travelled toward us, and provoked a tiny vibration of space-time which was in turn responsible for a tiny deformation of the detector located on Earth. That deformation was measured due to highly advanced technologies based on laser interferometry. It is a technique capable of measuring the interference of two laser beams and is thus able to monitor minute changes in distances with extremely high precision. The detector itself is a giant interferometer with arms of 4 kilometer in length. The same signal was observed a few milliseconds later by the other LIGO detector LIGO located in the American northwest, in the state of Washington. The difference between the arrival times of the signals onto both detectors provides information on the direction of the event in the sky.
The gravitational wave was immediately recorded upon the arrival of the signal, as an image in the so-called "time-frequency" diagram, which permits researchers to rapidly select interesting events as a characteristic increase of the frequency with time (Figure 3). The amplitude of the gravitational wave, which measures the space-time distortion causing for the detector's vibration, has then been directly measured (Fig GW150914). During the on-line analysis, performed simultaneously with the real time measurement of the signal, the algorithms of data analysis determined that the combination of the two masses which parametrizes the waveform in first approximation is too large for the signal to be due to the merger of neutron stars[2]. The event was therefore due to the merger of a pair black holes, illustrated using a numerical simulation in Figure 4. The most probable masses of the two black holes, determined from an analysis performed off-line, are respectively 36 and 29 times the mass of the Sun (Figure 5). These values are significantly larger than the masses of the known black holes in our galaxy, which are of stellar origin, that are produced by explosions of stars called supernovae. This result calls into question the current models of stellar evolution and how the population of very massive stars could have led to the formation of such relatively large black holes.
The distance of the region in the Universe where the coalescence happened is 1.3 billions of light years or approximately 400 megaparsec. This corresponds to a cosmological redshift of the order of 0.1, which means that the recession velocity of galaxies at that distance in the expanding Universe is about a tenth of the speed of light. Although there are many galaxies located up to such distances, it is nevertheless relatively nearby with respect to the very large distances (so called "cosmological distances"), over which further gravitational wave observations will explore.
The distance of the source emitting the gravitational wave can be directly inferred from a combination of the wave amplitude and the growth of its frequency. With a source at a distance of 400 megaparsecs, the gravitational amplitude is of the order of 10-21, which represents exactly the tiny relative displacement of the 4 km long arms of the detector during the passage of the wave. The signal to noise ratio, i.e. the ratio between the physical signal and the noise in the detector, that is the sum of all the noises caused by the detector's instruments as well as by the terrestrial environment, is approximately 25. The probability that the signal might be due to a statistical fluctuation of the noise (this is called the "false alarm" probability) is less than one over 10 millions (i.e. 10-7, which corresponds, in the statistical jargon, to a 5 "gaussian sigma" detection). The detection of GW150914 is therefore robust and unambiguous!
At the time when the two black holes were dectected, that is when the frequency of the gravitational wave signal entered the frequency bandwidth of the detectors at nearly 35 Hz (Figure 2), they were separated from each other by approximately 1000 km. The radius of each of the black holes is of the order of 100 km. During the fraction of a second that the event lasted (a fifth of a second), they orbited ten times on an inspiraling trajectory, with the two objects getting closer to each other because of the energy loss by gravitational radiation. Prior to the coalescence, the velocity of the black holes on their orbit reached half the speed of light! The signal frequency at the instant of coalescence is 150 Hz(Figure 2), which is close to the sensitivity peak of the detectors. The two black holes finally formed a single massive black hole, highly deformed because of the collision, but which then "relaxed" toward a stationary black hole by dissipation of energy in the form of gravitational radiation. This gravitational wave emission operated in the "quasi-normal" modes of the black hole, which are the characteristic resonance modes of a black hole. When the black hole has emitted all its quasi-normal modes, it becomes a "Kerr black hole", entirely characterized in general relativity by its mass and its rotation (or "spin"). In the case of GW150914, the mass of the final Kerr black hole is 62 solar masses and its spin, i.e. the angular momentum associated with the rotation velocity of the surface of the black hole, is estimated to be 0.7 in units of the speed of light (the maximum possible spin is one).
The difference between the sum of the masses of the two initial black holes and that of the final Kerr black hole is approximately 3 solar masses. What happened to this mass? It was converted into pure gravitational energy and taken away in a fraction of second by the gravitational wave! One can thus estimate the power of this event as being 1055 erg per second, which is the equivalent of the total energy of about 1000 supernovae explosions released in a fraction of seconds, an enormous amount.
Contribution of theory to this discovery
Thanks to the high signal-to-noise ratio and to the maximal frequency being in the best sensitivity band of the detectors, this outstanding event gives us access to the three successive phases of the coalescence, namely the initial inspiraling phase comprising about ten orbital cycles, the very short merger phase and finally the relaxation (or so-called "ringdown") phase of the newly formed black hole (Figure 6). The analysis of the signal in these three phases revealed that it is in excellent agreement with the expectation from general relativity. No deviation with respect to this theory is found.
The consistency between the observed signal and that predicted by theory obviously is an extremely important ingredient of the detection process. Indeed, such a discovery can only be claimed if one is convinced that the signal corresponds to a real physical phenomenon expected from theory, and possibly accurately computed. Without the theory, no detection is possible because any un-modeled signal (for which we have no physical interpretation) can always be seen as due to a statistical fluctuation of the noise in the detector.
One of the greatest interest of binary systems[3] of compact objects (either neutron stars or black holes), is that the gravitational waves they emit can be computed within general relativity with high accuracy. It can be shown that all non gravitational effects, which generally plague the dynamics of ordinary star systems (such as the presence of an accretion disk around stars, the effects of the interstellar medium and magnetic fields, or even the internal structure of dense matter inside neutron stars), play a negligible impact on the dynamics and radiation of compact objects. The problem to solve is therefore the gravitational two-body problem in general relativity.
In the initial inspiraling phase, the compact objects are quite far apart from each other, their orbital velocity is small with respect to the speed of light, and the system can be modelled by two point masses. The gravitational wave is then computed thanks to the so-called "post-Newtonian" approximation, which is an expansion of general relativity when the velocity of the objects is small compared to the speed of light. In this limit, general relativity tends to Newton's theory. The post-Newtonian approximation has been at the origin of most of the great successes of general relativity in the past, when comparing its predictions to actual observations (such as the relativistic advance of the perihelion of planet Mercury, and the deviation of light rays by the Sun). In the case of gravitational waves from inspiraling compact binaries, the post-Newtonian approximation is an expansion of the wave in a series of approximations beyond the Einstein quadrupole formula (Figure 1). It turned out that it was necessary to develop the approximation series up to very high precision.
Starting from the 1990's, physicists at the IAP and their collaborators have developed a new formalism for calculating the gravitational waves emitted by isolated matter systems in general relativity, and applied it to the problem of inspiraling compact binary systems. The outcome of these calculations in a highly accurate post-Newtonian prediction, taking the form of mathematical expressions, which are now used in all gravitational wave detectors for searching and analyzing the signal from merging compact binary systems, in their inspiraling phase.
When the two compact objects make contact and merge, the post-Newtonian approximation is no longer valid. In the merger phase, the prediction from general relativity must be determined using gigantic numerical simulations with computers. For a long time, these numerical simulations posed an actual challenge to the physicists, but they were finally resolved in 2005. On the other hand, the numerical calculations are not appropriate in the inspiraling phase because of prohibitively long computing times. Thus, the physicists now have access of an "exact" numerical solution for the merger phase, also valid for the "ring-down" phase (much like a bell after being struck). This numerical solution connects with high accuracy to the post-Newtonian solution describing the inspiraling phase (Figure 6). Other analytical methods have also been developed, which result in replacing the actual physical two body problem (thanks to techniques of "resummation" of the post-Newtonian series) with a simpler "effective one body" (EOB) problem. This approach has been confirmed and improved with the numerical calculations by computer. The data analysis of the experiments such as the LIGO/VIRGO collaboration uses this type of effective method, as it is very useful in practice for exploring in real-time, that is at the moment of detection, a large region of the parameter space (in particular the black holes masses).
To conclude, the problem of the coalescence of compact objects in general relativity is solved by the combination of the analytic post-Newtonian approximation method, very accurate for large separations but failing at the instant of the merger, and of exact numerical simulations for the last merger and ring-down phases. It is this solution which is used for searching and analyzing the gravitational wave signals.
In the case of large black hole masses like in GW150914, the major part of the detection occurs in the merger phase of the black holes, therefore the numerical prediction plays the most important role. Indeed, one observes only a few orbital cycles before the coalescence (Figure 5). But in the case of less massive black holes or in the case of binary systems of neutron stars (a source of gravitational waves that researchers are almost certain to observe at least once a year with LIGO, according to the number of known binary pulsars in our galaxy), the signal-to-noise ratio will be mostly due to the inspiraling phase, made of thousands of observable orbital cycles. The post-Newtonian approximation will then play a crucial role.
Notes
[1] A black hole is an object which is so compact that its gravitational field prevents any matter or radiation to escape from it. Such an object cannot emit or reflect light, and is in principle black. However, this is true only within the classical theory of general relativity: we know, since the work of Hawking, that a black hole does emit radiation because of quantum physical effects; but this radiation is negligible for black holes with large masses like in GW150914.[2] A neutron star is what remains of a massive star when it explodes as a supernova. It is made of neutrons held together by gravitation. A neutron star is hardly detectable, except if it manifests itself by pulsed radio emission (it is then called a pulsar), or by the presence of an accretion disk of matter which has been tidally torn from a companion star.
[3] In astronomy, a binary system is composed of two objects of the Universe linked by the gravitational force. The objects follow a bound orbit around their common center of mass.
Link
Writing and contact
- Luc Blanchet
Institut d’astrophysique de Paris, CNRS, UPMC
luc [dot] blanchet [at] iap [dot] fr
- Guillaume Faye
Institut d’astrophysique de Paris, CNRS, UPMC
guillaume [dot] faye [at] iap [dot] fr
Layout: Jean Mouette
Figures
Figure 1


One year after his formulation of the theory of general relativity, in November 1915, Einstein predicted the existence of gravitational waves. Then, in 1918, he obtained the famous "quadrupole" formula which gives the amount of energy carried away by a matter system in the form of gravitational waves. The proof of the existence of gravitational waves (and of the validity of the quadrupole formula) was obtained in 1979, with the observation of the decay of the orbit of the binary pulsar PSR 1913+16 discovered by Hulse and Taylor (Nobel prize in 1993). Credits: DR.
Figure 2
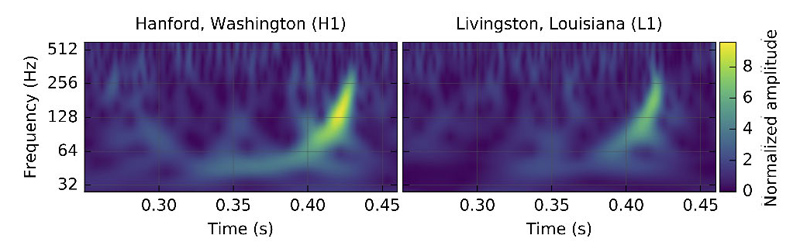
The gravitational wave observed by the two LIGO detectors in Hanford and Livingstone in a diagram giving the evolution of frequency with time. For a wave, the frequency is the number of oscillations per second. In the case of a gravitational wave, the growth of the frequency with time (with the shape of a "giraffe") is a characteristic feature of the coalescence of two compact objects. Credits: collaboration LIGO/VIRGO.
Figure 3
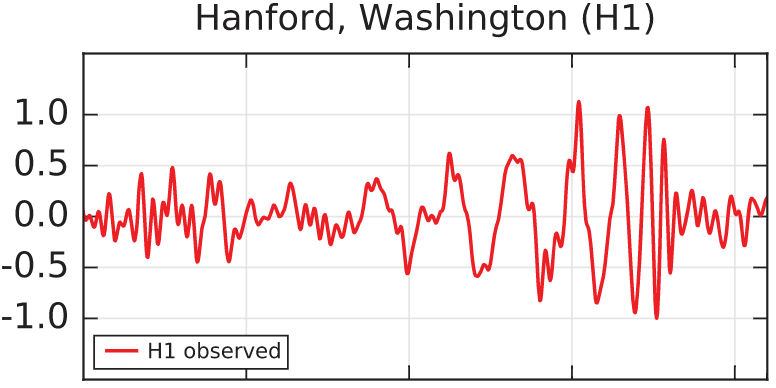
Upper panel: the signal observed by the LIGO detector located in Hanford, in unit of 10-21 times the relative variation of the length of the arms of the interferometer.
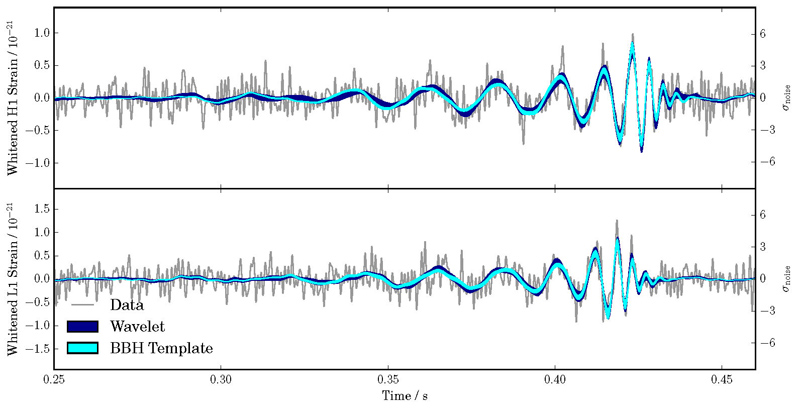
Lower panel: The two signals observed on the two sites of Hanford and Livingstone. The arrival times of the two signals are separated by 7 milliseconds. In blue is shown the fit of the data by a wavelet (which is a mathematical description of the signal, without any physics) and in cyan the best gravitational wave "template", which represents the physical prediction of the theory of general relativity. Credits: collaboration LIGO/VIRGO.
Figure 4

A binary system of two black holes very close to the final coalescence. The strong gravitational field of the black holes distorts the images of the stars located in the background, by the effect of gravitational bending of light. Credits: SXS - Simulating eXtreme Spacetimes.
Figure 5
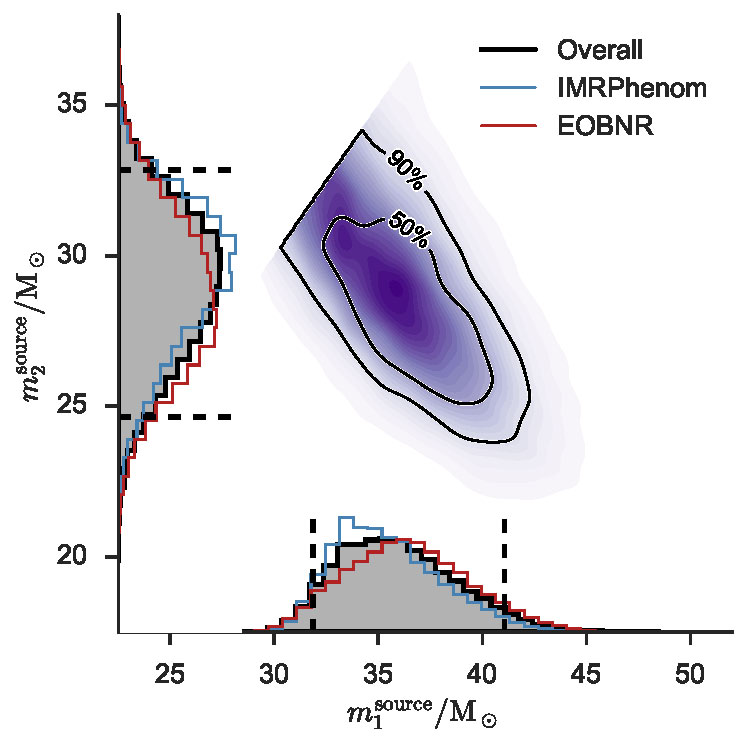
The masses of the black holes are measured by comparison with the theoretical predictions combining analytic and numerical calculations in general relativity. The contour lines indicate the probability to have two simultaneous values for the masses m1 and m2 for the black holes. The curves along each axis show the probability distributions for the masses of each black hole. The peaks of these curves give the most probable values for GW150914, around 36 solar masses for m1, and 29 for m2, with an uncertainty of about 4 solar masses for each. Credits: collaboration LIGO/VIRGO.
Figure 6
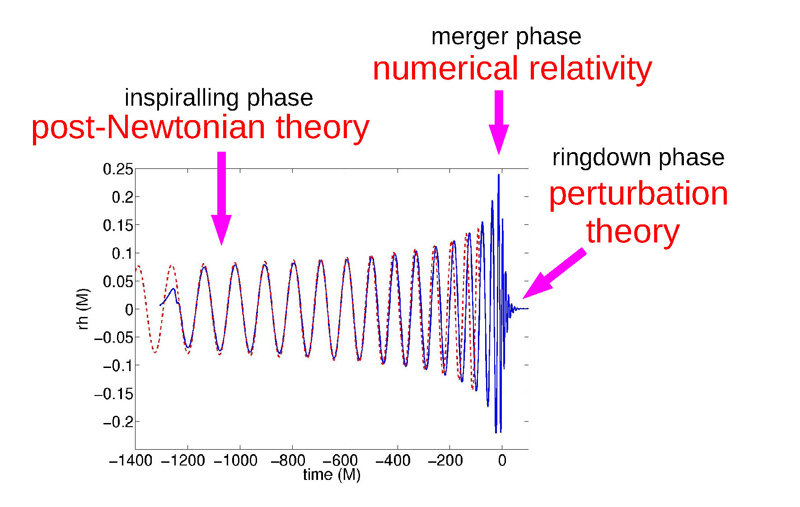
The gravitational wave amplitude in the three phases of the coalescence of a compact binary system, and the methods used to determine it. The post-Newtonian calculation is valid in the inspiraling phase and is shown as a red dashed line. It is matched with the numerical calculation valid in the merger and ring-down phases, which is shown as a blue line. Alternatively, the "effective one body" (EOB) formalism combines the results from numerical relativity with perturbation theory for the final phases, while it matches with the post-Newtonian calculation for the initial inspiraling phase.
March 2016
