DISCOVERING THE ORIGINS OF THE UNIVERSE THANKS TO A MATHEMATICAL TIME MACHINE
Combined progress in cosmology, mathematics and computer science carried out by a multidisciplinary team has made it possible to build a new mathematical method which has the potential to shed new light on the formation of structures throughout the history of the Universe. The article describing this method by Sebastian von Hausegger (University of Oxford), Bruno Lévy (Université de Lorraine, Inria, LORIA) and Roya Mohayaee (IAP, CNRS, Sorbonne Université), was published in Physical Review Letters, and was selected by Physics magazine, which highlights landmark results in physics.
This new method makes it possible to go back in time from a three-dimensional map of the cosmos, and to reconstruct backwards the movements of all the galaxies (and on a larger scale, of their arrangement: the large-scale structure of the Universe), starting from the present time until the origin of the Universe (13.7 billion years ago); this is done assuming that originally the Universe was much hotter, much denser and much more homogeneous than now (the Big Bang model).
To build this method, the multidisciplinary team has worked throughout the last 7 years to develop a common language between physics, mathematics and computer science. The starting point is the principle of least action, which describes the evolution of a physical system as a "shortest path" in space and time. For example, a well-known case of this principle implies that electricity always takes the shortest path. In general, according to this principle, the trajectories of the points of a system, defined by the positions and velocities as a function of time, are those for which a quantity called "the action integral" is minimal. To reconstruct the history of the Universe (in the context of gravitation), the idea is to translate this physical principle into a computer, and which can operate in reverse, that is to say going back in time. What makes it possible to do optimal transport, a mathematical tool that the team is studying in collaboration with mathematician Yann Brenier (University of Paris-Saclay), one of the main inventors of this theory. This allowed them to highlight and exploit properties of the action integral, and thus lead to a new and very efficient method, which for the first time can be applied to hundreds of millions of galaxies.
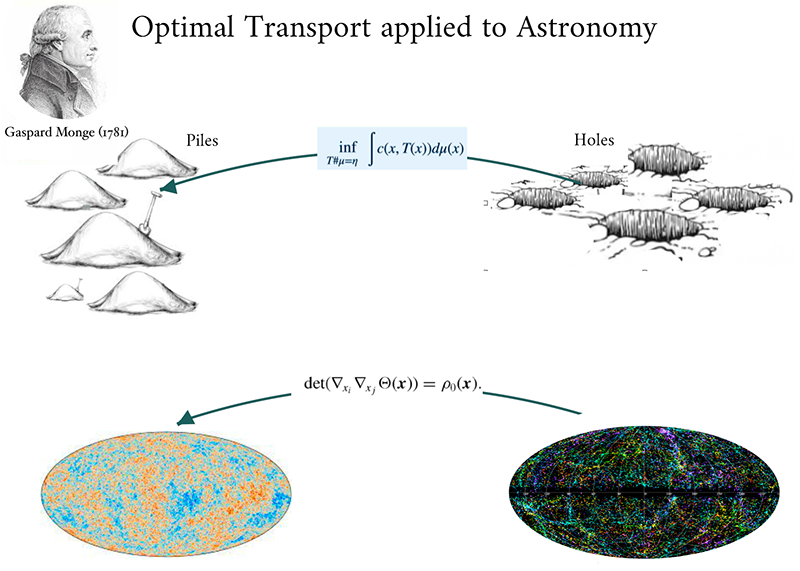 Figure 1:
Figure 1:
Top: The mass transportation problem, was initially formulated by Monge before the French revolution. In charge of drawing up plans for fortifications, Monge aimed at finding how to transport soil from a number N of excavated holes (“déblais”) to the same number of piles of rubble (“remblais”) while minimizing the total product of the transported mass and the travelled distance (Monge 1784). This problem has a rich mathematical structure that was revealed later by a continuous stream of advances in fundamental mathematics (see review by Villani (2009).
Bottom: The reconstruction problem in cosmology, that is how to go back in time and reconstruct the past history of the Universe and thereby details from the cosmic background emission starting from the sole knowledge of the present positions galaxies. This problem is formulated by the Monge-Ampère equation, the solution to which lies in the solution to the Monge's initial problem.
Credits: Carte Maximum, Beaune, 13/10/1990 - iStock.com/Annika Gandelheid - ESA and the Planck Collaboration - T.H. Jarrett (IPAC/SSC) - Roya Mohayaee
Optimal transport studies how to transport material from a set of positions (the “heaps” in Fig 1) to other positions (the “holes” in Fig 1) while minimizing the “effort”, defined as the product of the mass transported and the distance travelled. This problem was studied by Gaspard Monge, shortly before the French Revolution, in order to plan earthworks. This idea of minimizing a certain “effort” resembles the principle of least action, with the difference that the time variable does not appear in it. However, in certain very specific cases, the time variable disappears and the two problems become equivalent. In the case of the reconstruction of the history of the Universe, minimizing the action amounts to a first approximation to minimizing the kinetic energy, which implies that all the particles move in a straight line at constant speed. Under this hypothesis, the only question that remains to be determined is which particle comes from which initial position. Thus, the action minimization problem becomes equivalent to the optimal transport problem (Benamou, Brenier 2000). Once the initial and final positions of the trajectories are determined, it is then possible to take into account more complex movements of the particles, for example by integrating the terms of the action corresponding to the expansion of the Universe.
Roya Mohayaee, CNRS researcher at the Paris Institute of Astrophysics, was a pioneer in formulating the problem of reconstructing the history of the Universe in terms of optimal transport theory, when, back in 2002, she collaborated with Yann Brenier as well as with physicists and cosmologists Michel Hénon, Uriel Frisch, Sabino Matarrese and Andrei Sobolevski. But the efficiency of the algorithms available at the time did not allow them to be applied to large amounts of data to model the distribution of matter in the Universe with sufficient precision. Advances in the field of digital sciences, and the expertise of Bruno Lévy (Université de Lorraine, Inria, LORIA), director of the Inria Nancy Grand-Est center, particularly in digital geometry, allowed the development of a new algorithm and its implementation in the form of very efficient programs.
The new method uses a particular formulation of optimal transport, called semi-discrete, because it transports a uniform and continuous distribution of matter towards a discrete set of points. This formulation has two advantages: (1) on the one hand, it corresponds exactly to the context of the cosmological reconstruction, which assumes a homogeneous initial condition, and a final condition where the matter has condensed into galaxies and clusters of galaxies, represented at this scale by points. (2) on the other hand, by exploiting its mathematical structure (the function optimized by the method is regular, i.e. all its derivatives are continuous, and it is concave, i.e. any segment connecting 2 points of the function is below this one, which implies a single maximum). Moreover, since it transports regions of space rather than individual points, the numerical algorithm is much faster than previous methods. Thus, for the first time, it can be applied to hundreds of millions of galaxies. It determines the structure of the regions of space that have collapsed to form each galaxy. These regions form a mathematical object (called a Laguerre diagram), which can be calculated exactly, thanks to specialized algorithms. Figure 2 shows the final state of a simulation of a region of the Universe comprising 180 million galaxies, and on the right a zoom on a part of the Laguerre diagram corresponding to the reconstructed initial conditions (the complete Laguerre diagram is made of 180 million regions). Once the initial condition is reconstructed, by minimizing the action integral, it is possible to reconstruct the trajectories of the galaxies. In Figure 3, one can see the reconstructed trajectories, here from 2-dimensional simulation, in order to facilitate the visualization of the trajectories. An animation of this reconstruction is shown in the video below.
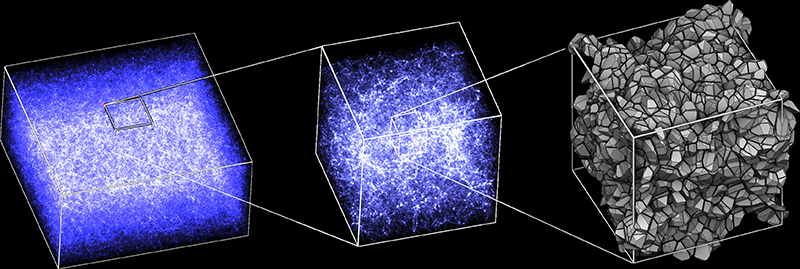 Figure 2: Reconstruction of a region of the Universe using the optimal transport method.
Figure 2: Reconstruction of a region of the Universe using the optimal transport method.
Left: 3-dimensional simulation of a region of the Universe containing 180 million galaxies, each represented by a point.
Center: Zoom of left image within a cube.
Right: New zoom into the central image, but this time showing the reconstructed initial conditions, i.e. indicating for each galaxy of the new central sub-cube the area of space from which its material originated; this is a Laguerre diagram, in which each polyhedron corresponds to one among the 180 million regions of space that collapsed to form a galaxy.
Credit: Bruno Lévy
 Figure 3: Example of the reconstruction in 2 dimensions.
Figure 3: Example of the reconstruction in 2 dimensions.
Left: Simulation of the observation of the positions of the galaxies at the present time.
Center: Initial matter material density fluctuations reconstructed by the optimal transport method from the map on the left.
Right: The reconstruction also produces the trajectories of the galaxies that led to the map on the left.
Credit: Bruno Lévy
The method has the potential to provide a better understanding of the formation of large structures in the Universe, by linking what we observe today with the phenomena that occurred during the first 380,000 years of the Universe's existence, when it was in the form of plasma (see Box 1).
1. The primordial plasmaAt the very beginning, the Universe looked like a gigantic star, entirely in the form of a plasma mixing the components of atomic nuclei, protons and neutrons, and electrons, which normally constitute atoms, but here were moving freely in the plasma due to its very high temperature. Two forces were then in balance: gravity, tending to make matter collapse on itself, and light (electromagnetic force), exerting a “pressure” opposing this collapse. Indeed, even if the photons that make up light have no mass, they transfer energy to the atomic nuclei when they collide with them. The overall effect of these photons is the same as the pressure of a liquid, which prevents it from compressing (in stars, in which the same phenomenon takes place, it is called hydrostatic equilibrium). During these first 380,000 years, electrons were free to move, and their frequent interactions with photons made far propagation of light impossible: the Universe was therefore opaque. |
The original plasma was not perfectly uniform, but contained small local variations in density, very weak, about one 100,000th of the average density). By the combined effect of the force of gravity and the pressure exerted by light, these variations in density led to the propagation of pressure waves, of the same nature as sound waves, called baryon acoustic oscillations (BAO; the baryons designating the protons, neutrons and electrons present in the atomic nuclei). The spatial distribution of these variations became “frozen” in matter at the time of recombination, when light ceased to interact closely with matter (see Box 2). In the cosmic background radiation, we measure both the small initial density variations, and the imprint of the acoustic oscillations of the baryons, which could be measured very precisely by the Planck satellite. The imprint of the acoustic oscillations of the baryons then evolved over time, subject to the influence of gravity and the expansion of the Universe, until being reflected in the distribution of galaxies and large structures (galaxy clusters and superclusters). Thus, this imprint has been scrambled and considerably attenuated by gravity during the approximately 13.7 billion years of evolutionary history of the Universe after recombination..
2. The cosmic background radiationAfter 380,000 years, the plasma had cooled enough for atomic nuclei to capture electrons (known as “recombination”) and form mostly hydrogen atoms. Electrons stopped scattering the photons, which thus were able to escape: the Universe became transparent, permeable to light. The light emitted at that time is still detected today. It now appears as radiation in the microwave range (the cosmic microwave background). This radiation is responsible for a good part of the interference observed on an old analogue television. |
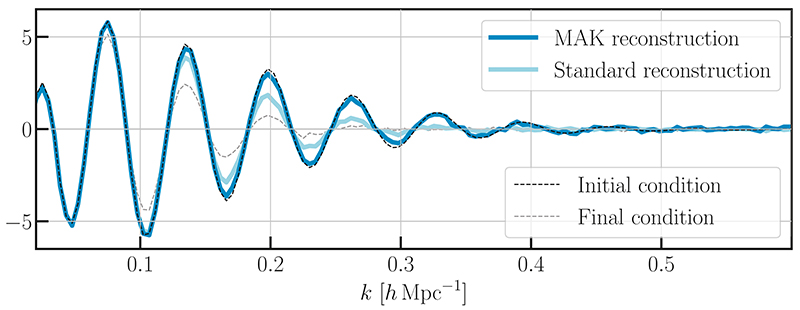
By making it possible to "go back in time" to a map of the density of matter in the Universe, the new method makes it possible to reconstruct with great precision the initial signal corresponding to the acoustic waves. A set of tests on numerical simulations of the evolution of the Universe carried out by Sebastian von Hausegger (post-doctoral research fellow at the Rudolf Peierls Center for Theoretical Physics at the University of Oxford) show that this reconstruction is visibly more precise (see Fig. 4) than the so-called "standard" reconstruction method that was originally devised by of Eisenstein, Seo, Sirko and Spergel, and is commonly used to date. Sandard reconstruction uses an approximation of the density fields by smoothing (allowing the reduction of irregularities and singularities), and does not have the same mathematical properties as the new method (regular and concave function). The new method will eventually make it possible to relate this profile of acoustic waves reconstructed from the distribution of matter at the present time, with that measured in the cosmic background radiation. Thus, this method has the potential to offer a new investigative tool to try to answer several questions. There are still big open questions in cosmology, namely about the laws of physics that govern the history of the Universe and the formation of its large-scale structures. For example, calculations and indirect observations suggest that we can only directly detect 10% of the matter present in galaxies. The remaining 90% (which has been called "dark matter") resists any means of direct detection. It is not yet clear whether it is exotic matter that does not interact directly with baryons or light, or whether the laws of gravitation and general relativity must be questioned. On the other hand, we know since the 90s that the expansion of the Universe has considerably accelerated during the last 4 billion years. To bring the equations of the model into line with reality, it was necessary to reintroduce into the equations of General Relativity a term that Einstein had abandoned (the cosmological constant), it was given the name of dark energy, yet its nature is still unknown. Since the profiles of the acoustic waves are dependent on the models of dark matter and dark energy, the new tool will make it possible to pose constraints on these models.
 |
Video: Animation of the 2-dimensional matter distribution of Fig. 3 at all epochs from the initial conditions to the present time, reconstructed by the optimal transport method.
Credit: Bruno Lévy
Credits: Sebastian von Hausegger, Bruno Lévy, Roya Mohayaee
Motivated by the conviction that important discoveries are to be made at the border of the three disciplines that form physics, mathematics and computer science, the researchers of the team continue to explore the applications of optimal transport in cosmology. They plan to apply their method to upcoming and future observational data from the Dark Energy Spectroscopic Instrument (DESI) at the Kitt Peak National Observatory, from ESA's Euclid probe, and the LSST Vera Rubin observatory (expected to be operational in 2023). These surveys will provide new extended maps of the distribution of galaxies in three dimensions (of the type of the simulation of Fig. 2), which the optimal transport method will use to go back in time and deduce the baryonic acoustic oscillations, testing different models of dark matter and dark energy.
Links
![]() Article in Physical Review Letters: von Hausegger, Lévy, Mohayaee, 2022, “Accurate Baryon Acoustic Oscillations reconstruction via semi-discrete optimal transport” (Public version)
Article in Physical Review Letters: von Hausegger, Lévy, Mohayaee, 2022, “Accurate Baryon Acoustic Oscillations reconstruction via semi-discrete optimal transport” (Public version)
![]() Article in Physics: Wright, 2022, “Turning Back Time on Space”
Article in Physics: Wright, 2022, “Turning Back Time on Space”
![]() Article in Monthly Notices of the Royal Astronomical Society : Lévy, Mohayaee, von Hausegger, 2021, « A fast semi-discrete optimal transport algorithm for a unique reconstruction of the early Universe » (Public version)
Article in Monthly Notices of the Royal Astronomical Society : Lévy, Mohayaee, von Hausegger, 2021, « A fast semi-discrete optimal transport algorithm for a unique reconstruction of the early Universe » (Public version)
![]() Article in Numerische Mathematik: Benamou, Brenier, 2000, “A computational fluid mechanics solution to the Monge-Kantorovich mass transfer problem” (PDF)
Article in Numerische Mathematik: Benamou, Brenier, 2000, “A computational fluid mechanics solution to the Monge-Kantorovich mass transfer problem” (PDF)
![]() Article (in French) in Images des Mathématiques: Brenier, Viéville, 2012, “La brouette de Monge ou le transport optimal”
Article (in French) in Images des Mathématiques: Brenier, Viéville, 2012, “La brouette de Monge ou le transport optimal”
Reference
![]() Book: Villani, 2003, “Topics in Optimal Transportation” (Graduate Studies in Mathematics, American Mathematical Society)
Book: Villani, 2003, “Topics in Optimal Transportation” (Graduate Studies in Mathematics, American Mathematical Society)
Writing and contacts
- Bruno Lévy
Université de Lorraine, Inria, Laboratoire lorrain de recherche en informatique et ses applications (LORIA)
bruno.levy[at] inria [point] fr - Roya Mohayaee
Institut d’astrophysique de Paris, CNRS, Sorbonne Université
roya.mohayaee [at] iap [dot] fr - Sebastian von Hausegger
Rudolf Peierls Center for Theoretical Physics, University of Oxford
sebastian.vonhausegger [at] physics [dot] ox [dot] ac [dot] uk
Web writing: Valérie de Lapparent
Layout and iconography: Jean Mouette
August 2022
