Research
Broadly speaking, my work involves using insights from theoretical high-energy physics to explore the early Universe. My interests span a wide range of topics, from the physics of the early Universe to modern quantum field theory techniques and observational aspects in cosmology. I also have strong numerical skills. Below is an overview of my main research topics and interests. To avoid clutter, references have been omitted.
- Primordial Cosmology through the lens of Cosmological Correlators
- Cosmological Flow
- Phenomenology of Primordial non-Gaussianities
- Modern Quantum Field Theory Techniques for Cosmology
- Effective Field Theory Techniques
- Other Interests
The first section is designed for a general audience, while the following sections are aimed at aficionados and experts.
Primordial Cosmology through the lens of Cosmological Correlators
Linking cosmological observations to theoretical high-energy physics (for a general audience)
 Our Universe on Large Scales. When we look at the night sky, most of the twinkling dots we see are nearby stars within our own galaxy, the Milky Way. At first glance, these stars seem scattered randomly, with some areas densely populated and others nearly empty. Ancient civilisations, like the Greeks, even noticed patterns and named constellations based on them. But there's much more to the cosmos than meets the eye. If we could zoom out, we would discover even more dots—these would be stars from galaxies beyond our own. Zoom out further, and an entire galaxy, with its tens of millions of stars, would shrink to a single dot. And as we continue zooming out, these dots—representing galaxies—begin to form what we call the Large-Scale Structure of the Universe, a vast web of galaxy clusters and empty spaces called voids.
Our Universe on Large Scales. When we look at the night sky, most of the twinkling dots we see are nearby stars within our own galaxy, the Milky Way. At first glance, these stars seem scattered randomly, with some areas densely populated and others nearly empty. Ancient civilisations, like the Greeks, even noticed patterns and named constellations based on them. But there's much more to the cosmos than meets the eye. If we could zoom out, we would discover even more dots—these would be stars from galaxies beyond our own. Zoom out further, and an entire galaxy, with its tens of millions of stars, would shrink to a single dot. And as we continue zooming out, these dots—representing galaxies—begin to form what we call the Large-Scale Structure of the Universe, a vast web of galaxy clusters and empty spaces called voids.
Back in Time. Remarkably, on large scales, the Universe appears to be both homogeneous and isotropic. This means that, no matter where we are or which direction we look, these cosmological structures seem roughly similar. These structures are the result of billions of years of time evolution under the effect of gravity, as tiny initial fluctuations gradually collapsed to form galaxies. But how do we know this? Because light travels at a finite speed, when we observe distant objects in the sky, we are actually looking back in time. The farther away something is, the older the light we are seeing. Using this incredible fact, cosmology aims to piece together the Universe’s history from its earliest moments to the large-scale structures we observe today.
Quantum Origin of Structure. A natural question that arises is: where did these initial fluctuations come from? The most plausible explanation we have today is quite astonishing! Based on detailed analysis of cosmological data, we believe that the early Universe experienced a very brief but intense phase of accelerated expansion, known as inflation. This expansion was so immense that tiny quantum scales were stretched to cosmic scales. According to quantum physics, even empty space isn’t truly empty—it contains tiny, fleeting "wiggles" called quantum fluctuations that constantly appear and vanish almost instantly. During inflation, these quantum fluctuations were amplified into macroscopic density fluctuations, which eventually became the structures we observe today.
 Laboratory for High-Energy Physics. Although there is strong evidence supporting inflation, much about its underlying physics remains a mystery. For instance, we don't know exactly what particles were at work during that time nor how they interacted. There is one main reason for this. Inflation is believed to have occurred at an incredibly high energy scale, far beyond what our most powerful ground-based particle collider experiments can replicate. This means we cannot safely extend our current theories to that early phase of the Universe. But rather than being a limitation, this is actually an exciting opportunity! The early Universe might have left behind clues—through late-time observations—that hint at potential new physics in a completely unexplored high-energy regime.
Laboratory for High-Energy Physics. Although there is strong evidence supporting inflation, much about its underlying physics remains a mystery. For instance, we don't know exactly what particles were at work during that time nor how they interacted. There is one main reason for this. Inflation is believed to have occurred at an incredibly high energy scale, far beyond what our most powerful ground-based particle collider experiments can replicate. This means we cannot safely extend our current theories to that early phase of the Universe. But rather than being a limitation, this is actually an exciting opportunity! The early Universe might have left behind clues—through late-time observations—that hint at potential new physics in a completely unexplored high-energy regime.
Observing rather than Experimenting. You might rightly wonder how we can even study the physics of inflation and test our theories. In typical particle collider experiments, fundamental laws of Nature (such as the properties of elementary particles like their masses) are probed by smashing particles together and examining the resulting debris. These high-energy collisions create new particles, which can then be detected and measured. The particles we detect provide insight into what occurred during the collision. However, importantly, fundamental particles are governed by quantum principles, which are probablistic, and we can’t predict outcomes with certainty. The objects we measure are called cross sections, and tell us about how probable a certain process is. It means that we need to perform a lot of collisions to be able to correctly extract the physical properties of elementary particles. This is of course impossible in cosmology, as the history of the Universe only unfolded once. Instead, we use a different approach: we observe in different directions in the sky. By measuring specific signals or objects in different parts of the sky, we collect data as if they were coming from independent experiments. Assuming that the laws of physics are the same everywhere in the Universe, we are able to extract information about the physical processes that shaped the cosmos. In essence, where particle physics relies on averaging over many experiments, cosmology is all about performing statistical analysis over many observations.
 Cosmological Correlators. We cannot predict the exact position of galaxies in the Universe. However, a question we might ask is: what is the probablity of finding a galaxy at a certain distance from another one? By asking this for various distances, we construct something called the two-point correlation function. If all the information about the physics is captured by this function, we say the observed correlations are Gaussian. In other terms, the histogram of observed fluctuations in the sky (the number of fluctuations of a given amplitude as a function of the amplitude) follows a Gaussian curve. However, this function only tells us about the overall amplitude of the fluctuations, not about the specific particles present in the early Universe nor how they interacted. In particle physics, this would be like watching a single particle freely moving without interacting with anything around it, missing out on a lot of interesting information. Instead, we need to look at the correlation between more than two points in the sky. These higher-point correlations deviate from a perfect Gaussian distribution and are known as non-Gaussianities. Remarkably, these cosmological correlators can be theoretically predicted and measured in the sky. This way, cosmological correlators are the key mathematical objects that link theory and observations.
Cosmological Correlators. We cannot predict the exact position of galaxies in the Universe. However, a question we might ask is: what is the probablity of finding a galaxy at a certain distance from another one? By asking this for various distances, we construct something called the two-point correlation function. If all the information about the physics is captured by this function, we say the observed correlations are Gaussian. In other terms, the histogram of observed fluctuations in the sky (the number of fluctuations of a given amplitude as a function of the amplitude) follows a Gaussian curve. However, this function only tells us about the overall amplitude of the fluctuations, not about the specific particles present in the early Universe nor how they interacted. In particle physics, this would be like watching a single particle freely moving without interacting with anything around it, missing out on a lot of interesting information. Instead, we need to look at the correlation between more than two points in the sky. These higher-point correlations deviate from a perfect Gaussian distribution and are known as non-Gaussianities. Remarkably, these cosmological correlators can be theoretically predicted and measured in the sky. This way, cosmological correlators are the key mathematical objects that link theory and observations.
Questions I ask myself. My research is a part of a long-term effort aiming at using these cosmological correlators to understand the physics of the early Universe. Broad questions I ask myself include: How to construct well motivated high-energy theories that describe the early Universe? How to efficiently compute these cosmological correlators? What is the mathematical structure of cosmological correlators? How do they encode new physics? How to precisely measure these signals in the sky? Are there other objects we can measure in the sky that also encode interesting physics?
Cosmological Flow
Automating the computation of cosmological correlators by tracing their time evolution (for aficionados and experts)
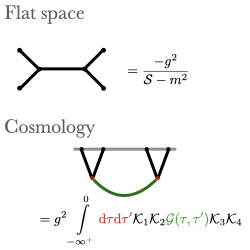 Daunting Complexity of Perturbation Theory. The spatial correlations of density fluctuations inherit in their structure all the information about the unknown and potentially new physics during inflation. Probing the early Universe through these cosmological correlators therefore requires measuring them with great precision and predicting them with high accuracy. In principle, computing cosmological correlators is a well-established procedure. It resembles computing Feynman diagrams in flat space. Given a theory, calculations can be carried out to arbitrary orders of perturbation theory. However, this standard procedure comes with its own set of challenges. Contrary to particle physics, interactions are not localised in time, and their effect needs to be tracked over the entire time evolution. The evolving background leads to additional (nested) time integrals to perform, and distorts the free propagation of fields. In the end, pushing forward the state-of-the-art of computational techniques, even at first order in perturbation theory, demands gruelling mathematical dexterity.
Daunting Complexity of Perturbation Theory. The spatial correlations of density fluctuations inherit in their structure all the information about the unknown and potentially new physics during inflation. Probing the early Universe through these cosmological correlators therefore requires measuring them with great precision and predicting them with high accuracy. In principle, computing cosmological correlators is a well-established procedure. It resembles computing Feynman diagrams in flat space. Given a theory, calculations can be carried out to arbitrary orders of perturbation theory. However, this standard procedure comes with its own set of challenges. Contrary to particle physics, interactions are not localised in time, and their effect needs to be tracked over the entire time evolution. The evolving background leads to additional (nested) time integrals to perform, and distorts the free propagation of fields. In the end, pushing forward the state-of-the-art of computational techniques, even at first order in perturbation theory, demands gruelling mathematical dexterity.
 Inspiration from Particle Physics. In particle physics, cross sections contain the dynamical information associated with the models used to describe data, and can be obtained from Feynman diagrams. From the theoretical side, probing fine features requires increasingly accurate predictions, and ensuring that all various possible processes are covered is a challenging task. Needless to say that the required precision imposes enormous demands on theory. Consequently, a large number of automated tools have been developed and are widely used by the community to make these accurate predictions. Numercial packages were designed to compute higher-order diagrams, to generate a large number of events for hadronic collider physics, or to automatically compute cross sections given Lagrangians as inputs. In cosmology, as computing correlators is extremely complex and relies on a case-by-case basis, the limited number of predictions can significantly skew our data interpretation. Therefore, there is a need for a tool that easily computes cosmological correlators in an automatic manner and for all processes.
Inspiration from Particle Physics. In particle physics, cross sections contain the dynamical information associated with the models used to describe data, and can be obtained from Feynman diagrams. From the theoretical side, probing fine features requires increasingly accurate predictions, and ensuring that all various possible processes are covered is a challenging task. Needless to say that the required precision imposes enormous demands on theory. Consequently, a large number of automated tools have been developed and are widely used by the community to make these accurate predictions. Numercial packages were designed to compute higher-order diagrams, to generate a large number of events for hadronic collider physics, or to automatically compute cross sections given Lagrangians as inputs. In cosmology, as computing correlators is extremely complex and relies on a case-by-case basis, the limited number of predictions can significantly skew our data interpretation. Therefore, there is a need for a tool that easily computes cosmological correlators in an automatic manner and for all processes.
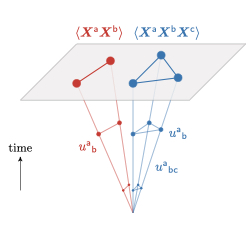 Cosmological Flow Approach. Cosmological correlators only depend on the specific theory active during inflation through how they "flow" towards the end of inflation. I have developed the cosmological flow approach that aims at automating this picture. This method is based on solving differential equations in time governing the time evolution of cosmological correlators, from their origin as quantum fluctuations in the deep past to the end of inflation. It takes into account all physical effects at tree level without approximation, and works for any theory. By shifting our focus in this way, we move beyond just calculating correlators for a few specific theories and open the door to exploring inflation in a much broader, more complete way.
Cosmological Flow Approach. Cosmological correlators only depend on the specific theory active during inflation through how they "flow" towards the end of inflation. I have developed the cosmological flow approach that aims at automating this picture. This method is based on solving differential equations in time governing the time evolution of cosmological correlators, from their origin as quantum fluctuations in the deep past to the end of inflation. It takes into account all physical effects at tree level without approximation, and works for any theory. By shifting our focus in this way, we move beyond just calculating correlators for a few specific theories and open the door to exploring inflation in a much broader, more complete way.
 CosmoFlow: Numerical Tool. I have developed CosmoFlow, an open source Python package designed to compute cosmological correlators using the cosmological flow approach. This code can efficiently compute any tree-level cosmological correlators in any theory and in all kinematic configurations. The main credo while developing CosmoFlow was simplicity! Whether you are theorists, primordial or late-time cosmologists, feel free to use it, as well as extending and/or improve some aspects of the code.
CosmoFlow: Numerical Tool. I have developed CosmoFlow, an open source Python package designed to compute cosmological correlators using the cosmological flow approach. This code can efficiently compute any tree-level cosmological correlators in any theory and in all kinematic configurations. The main credo while developing CosmoFlow was simplicity! Whether you are theorists, primordial or late-time cosmologists, feel free to use it, as well as extending and/or improve some aspects of the code.
 Applications. The cosmological flow approach paves the way for a far-reaching program of exploring the rich physics of the early Universe in light of upcoming cosmological observations. On observational grounds, it is expected that substantial progress is to be made in the coming years. These cosmological data will have the raw statistical power to precisely constrain cosmological correlators. With the cosmological flow, I aim at constructing a complete and unbiased theory/signature dictionary. The phenomenological interest of this program is that we are able to probe physical regimes that were completely out reach, and discover new signals. The long-term program is to create a bank of theoretical data to be nurtured by the work of the community. On the theory side, the cosmological flow opens up new directions in understanding fundamental physical principles like unitarity, and sheds light on the structure of differential equations satisfied by cosmological correlators, analogous to flat-space scattering amplitudes.
Applications. The cosmological flow approach paves the way for a far-reaching program of exploring the rich physics of the early Universe in light of upcoming cosmological observations. On observational grounds, it is expected that substantial progress is to be made in the coming years. These cosmological data will have the raw statistical power to precisely constrain cosmological correlators. With the cosmological flow, I aim at constructing a complete and unbiased theory/signature dictionary. The phenomenological interest of this program is that we are able to probe physical regimes that were completely out reach, and discover new signals. The long-term program is to create a bank of theoretical data to be nurtured by the work of the community. On the theory side, the cosmological flow opens up new directions in understanding fundamental physical principles like unitarity, and sheds light on the structure of differential equations satisfied by cosmological correlators, analogous to flat-space scattering amplitudes.
 Future direction. In cosmology, confronting theory against observations requires an accurate modelling. Powerful tools to make late-time predictions have been developed, such as Boltzmann solvers or N-body codes to simulate the non-linear Universe. My long-term and ambitious goal is to include the cosmological flow routine in the already-existing chain of late-time cosmological tools. This would automate the generation of theoretical primordial data that can be directly used for CMB or LSS observables, hence extending the cosmological flow to the late-time Universe.
Future direction. In cosmology, confronting theory against observations requires an accurate modelling. Powerful tools to make late-time predictions have been developed, such as Boltzmann solvers or N-body codes to simulate the non-linear Universe. My long-term and ambitious goal is to include the cosmological flow routine in the already-existing chain of late-time cosmological tools. This would automate the generation of theoretical primordial data that can be directly used for CMB or LSS observables, hence extending the cosmological flow to the late-time Universe.
For more details, see [Short Paper]
[Long Paper]
[Code Paper]
[Poster]
[Code]
Phenomenology of Primordial non-Gaussianities
Encoding the physics of the early Universe (for aficionados and experts)
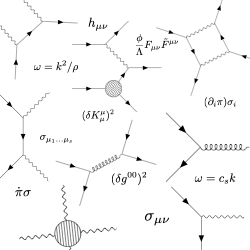
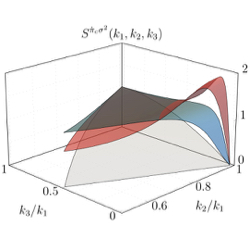 Shapes of Cosmological Correlators. Primordial density fluctuations can only be described in a statistical way, either by their complete probability distribution function, or equivalently by their correlation functions. Today, perfectly Gaussian initial fluctuations are still compatible with the data. That is to say, we have not (yet) detected deviations from perfect Gaussian statistics, the so-called non-Gaussianities. The reason is that these deviations are incredibly small! These non-Gaussianities, in the form of higher-point correlation functions, are a major target of future cosmological surveys as they encode the physics of the early Universe, like the number of particles active during inflation, together with their mass spectra, spins, sound speeds, and how they interact.
In spatial Fourier space, correlators are characterised by a running, an amplitude and a shape, that is how the signal depends on the mode wavenumbers. On large scales, fluctuations appear almost scale invariant so that the running does not contain much information. However, it might still hint at subtle changes in time during inflation, called features. The amplitude tells us about the overall strength of non-linearities, which is small. The shape, though, holds a wealth of information! Relating all the rich physics of the early Universe to the running, amplitude and the shape of cosmological correlators is quite an art, and it's an area where I have a lot of expertise.
Shapes of Cosmological Correlators. Primordial density fluctuations can only be described in a statistical way, either by their complete probability distribution function, or equivalently by their correlation functions. Today, perfectly Gaussian initial fluctuations are still compatible with the data. That is to say, we have not (yet) detected deviations from perfect Gaussian statistics, the so-called non-Gaussianities. The reason is that these deviations are incredibly small! These non-Gaussianities, in the form of higher-point correlation functions, are a major target of future cosmological surveys as they encode the physics of the early Universe, like the number of particles active during inflation, together with their mass spectra, spins, sound speeds, and how they interact.
In spatial Fourier space, correlators are characterised by a running, an amplitude and a shape, that is how the signal depends on the mode wavenumbers. On large scales, fluctuations appear almost scale invariant so that the running does not contain much information. However, it might still hint at subtle changes in time during inflation, called features. The amplitude tells us about the overall strength of non-linearities, which is small. The shape, though, holds a wealth of information! Relating all the rich physics of the early Universe to the running, amplitude and the shape of cosmological correlators is quite an art, and it's an area where I have a lot of expertise.
 Observational Program. Primordial non-Gaussianities have not been detected yet, but their detection is guaranteed just because gravity is intrinsically non-linear. It's only a matter of time before we find them! There's an ambitious observational effort underway. After the successful Planck survey, the next big step is to use three-dimensional large-scale structure surveys to improve our measurements. Upcoming galaxy surveys like Euclid, DESI, and LSST aim to enhance our current constraints by an order of magnitude. In the long run, 21cm intensity mapping surveys will further improve these measurements and help us reach the ultimate limits of what gravity can reveal, the so-called gravitational floor. Although distinguishing primordial non-Gaussianities from later-time non-linearities is definitely challenging, advances in machine learning techniques such as simulation-based inference and measuring non-Gaussianities at the map level give us hope for detecting highly informative signals.
Observational Program. Primordial non-Gaussianities have not been detected yet, but their detection is guaranteed just because gravity is intrinsically non-linear. It's only a matter of time before we find them! There's an ambitious observational effort underway. After the successful Planck survey, the next big step is to use three-dimensional large-scale structure surveys to improve our measurements. Upcoming galaxy surveys like Euclid, DESI, and LSST aim to enhance our current constraints by an order of magnitude. In the long run, 21cm intensity mapping surveys will further improve these measurements and help us reach the ultimate limits of what gravity can reveal, the so-called gravitational floor. Although distinguishing primordial non-Gaussianities from later-time non-linearities is definitely challenging, advances in machine learning techniques such as simulation-based inference and measuring non-Gaussianities at the map level give us hope for detecting highly informative signals.
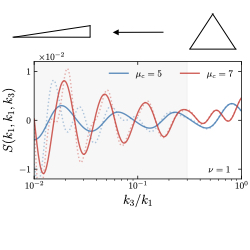 Cosmological Collider Physics. Observations indicate that the energy scale of inflation could have been as high as just a few orders of magnitudes below the Planck scale, marking the limit with the quantum gravity regime. This energy makes the study of the early Universe a unique opportunity to learn about potential new physics at the highest reachable energies, much higher than those achievable in ground-based experiments. This one-of-a-kind window to fundamental physics has opened a cosmological collider physics program. Essentially, even very heavy particles have been spontaneously produced in the early Universe, whose subsequent decays lead to imprints in cosmological correlators. These specific signatures could inform us about the inflationary particle content. As a concrete example, the presence and the mass of a heavy particle during inflation can be inferred from oscillatory patterns present in soft limits of cosmological correlators as we vary the kinematic configuration.
Cosmological Collider Physics. Observations indicate that the energy scale of inflation could have been as high as just a few orders of magnitudes below the Planck scale, marking the limit with the quantum gravity regime. This energy makes the study of the early Universe a unique opportunity to learn about potential new physics at the highest reachable energies, much higher than those achievable in ground-based experiments. This one-of-a-kind window to fundamental physics has opened a cosmological collider physics program. Essentially, even very heavy particles have been spontaneously produced in the early Universe, whose subsequent decays lead to imprints in cosmological correlators. These specific signatures could inform us about the inflationary particle content. As a concrete example, the presence and the mass of a heavy particle during inflation can be inferred from oscillatory patterns present in soft limits of cosmological correlators as we vary the kinematic configuration.
My Contributions. Motivated by the upcoming golden age of high-precision cosmological surveys, I am interested in developing the necessary theoretical techniques and discovering new signatures of potential new physics in cosmological correlators to interpret the future data. Signals of new physics in cosmological correlators depend on a lot of factors: the nature of the particle (mass, spin), the way they propagate (dispersion relation), the way particles interact and couple to each other (weak/strong mixing, weak/strong coupling, specific type of interactions), etc. My research aims at classifying all the possible signatures and find new robust and precise predictions of new physics. In this respect, I made several important contributions, as illustrated in the following examples:
Future Directions. The promising and rich phenomenology of non-Gaussianities invites us to extend the signals to more exchanged particles, and more complicated processes. For example, I aim at mapping out the would-be highly-dimensional phase diagram of all possible cosmological collider signatures in the complete theory of any number of exchanged scalar massive particles that would all mix among them. In the case of the bispectrum, where up to three particles can be exchanged in weak mixing scenarios, we still lack a complete solution for the full correlator. More complex processes, like calculating loop-level diagrams—especially challenging triangle and box diagrams—are also crucial. These diagrams are key because they reveal the underlying physics of fermions and gauge bosons. I also plan to propose a well motivated equilateral parity-odd trispectrum template. In the long term, I want to develop new computational techniques, such as dispersive or resummation techniques, to reconstruct what is known as the background signal (when exchanged heavy particles are integrated out). This signal is crucial because it often acts as background noise that hides the more interesting signals of new physics, so it must be subtracted in future data analyses. Ironically, it’s also one of the hardest signals to calculate. I also plan to probe the strongly coupled regime by importing non-perturbative techniques from conformal field theory, like numerical bootstrap, to cosmological correlators. Along these lines, I would like to derive accurate templates for the probability distribution of fluctuations itself (jargonically called wavefunction of the Universe) and explore non-perturbative formulations of non-Gaussianities beyond Feynman diagrams. The key question driving this program is: could there be signals we've missed?
For more details, see [Long Cosmological Flow Paper] [Parity Violation Paper] [Cosmological Low-Speed Collider Paper]
Modern Quantum Field Theory Techniques for Cosmology
Leveraging advanced QFT techniques to explore the foundations of early Universe theories (for aficionados and experts)
 Fundamental Principles. A revolutionary approach in modern quantum field theory (QFT) is the idea that the S-matrix, which describes particle interactions, can be fully determined by basic principles like symmetries, unitarity, crossing symmetry, and analyticity—without relying on the specifics of a dynamical theory. This means we can bypass traditional methods like computing Feynman diagrams and even Lagrangians. This concept, known as the bootstrap, originated with the discovery of the Veneziano amplitude, which helped kickstart string theory. Today, this method not only offers powerful computational tools, such as determining gluon scattering (like MHV amplitudes) and constraining strongly coupled theories, but it also provides deep insights into the structure of QFTs.
In cosmology, however, the understanding of cosmological correlation functions has not yet reached the same level of clarity. Despite this, progress is being made in uncovering the structure of these correlators. We now know the singularity structure of relatively simple correlators. Essentially, flat-space amplitudes are embedded in cosmological correlators as residues when the total energy of external particles adds up to zero. Likewise, when the energy of a subdiagram vanishes, the correlators factorise consistently. Additionally, unitarity, which reflects the conservation of probability at the quantum level, imposes a set of cutting rules. Recently, I introduced a new set of equations, called cosmological largest-time equations, that were secretly hidden in the Schwinger-Keldysh diagrammatics. These universal relations among correlators connect processes on different in-in branches through the analytic continuation of external energies, analogous to crossing symmetry in flat space.
My goal is to continue searching for universal rules that govern all cosmological correlators, with the ultimate aim of directly probing the fundamental principles of the Universe in the sky, rather than continuing mapping out the landscape of possible theories. For example, one intriguing question I’m interested in is: What kind of concrete cosmological observations could reveal a breakdown of unitarity (therefore hinting at e.g. dissipative processes) in theories of the early Universe?
Fundamental Principles. A revolutionary approach in modern quantum field theory (QFT) is the idea that the S-matrix, which describes particle interactions, can be fully determined by basic principles like symmetries, unitarity, crossing symmetry, and analyticity—without relying on the specifics of a dynamical theory. This means we can bypass traditional methods like computing Feynman diagrams and even Lagrangians. This concept, known as the bootstrap, originated with the discovery of the Veneziano amplitude, which helped kickstart string theory. Today, this method not only offers powerful computational tools, such as determining gluon scattering (like MHV amplitudes) and constraining strongly coupled theories, but it also provides deep insights into the structure of QFTs.
In cosmology, however, the understanding of cosmological correlation functions has not yet reached the same level of clarity. Despite this, progress is being made in uncovering the structure of these correlators. We now know the singularity structure of relatively simple correlators. Essentially, flat-space amplitudes are embedded in cosmological correlators as residues when the total energy of external particles adds up to zero. Likewise, when the energy of a subdiagram vanishes, the correlators factorise consistently. Additionally, unitarity, which reflects the conservation of probability at the quantum level, imposes a set of cutting rules. Recently, I introduced a new set of equations, called cosmological largest-time equations, that were secretly hidden in the Schwinger-Keldysh diagrammatics. These universal relations among correlators connect processes on different in-in branches through the analytic continuation of external energies, analogous to crossing symmetry in flat space.
My goal is to continue searching for universal rules that govern all cosmological correlators, with the ultimate aim of directly probing the fundamental principles of the Universe in the sky, rather than continuing mapping out the landscape of possible theories. For example, one intriguing question I’m interested in is: What kind of concrete cosmological observations could reveal a breakdown of unitarity (therefore hinting at e.g. dissipative processes) in theories of the early Universe?
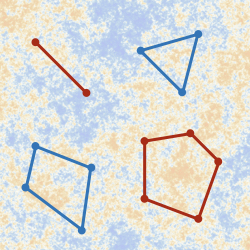
 Insights from Scattering Amplitudes. The true mathematical beauty of flat-space scattering amplitudes becomes clear when they are reinterpreted in auxiliary or dual spaces. For instance, exploring how causal dynamics is embedded in these amplitudes led to the discovery of new geometric structures like the amplituhedron. This structure generalises familiar shapes like triangles and polygons to higher-dimensional spaces. At the same time, scattering amplitudes admit Feynman integral representations, raising an intriguing question: what kinds of mathematical functions do these integrals generate? In flat space, loop integrals produce certain classes of iterated integrals and elliptic functions, with possible further generalisations. In cosmology, even the simplest tree-level correlators lead to more complex functions, such as polylogarithms and generalised hypergeometric functions.
One of the questions I'm interested in is: Can we formally study these function classes based on the properties of correlators? And conversely, can we learn something useful about correlators by studying the structures and behaviours of these functions? There are two related approaches to tackling this problem: the geometrical and dynamical perspectives.
Focusing solely on kinematics, the geometrical approach recognises that simple correlators can be seen as the canonical forms of a polytope, whose positive geometry makes properties such as locality and unitarity emergent. On the other hand, the dynamical approach examines the kinematic differential equations that these correlators satisfy. This growing field of research is revealing exciting connections between cosmological correlators and mathematical areas like twisted cohomology.
Rather than studying correlators directly in kinematic space, reformulating them in Mellin space transforms the problem into one of analysing higher-fold Mellin-Barnes integrals, whose solutions depend on triangulating a set of points. Different triangulations lead to various relationships between correlators, such as Euler's reflection identities. This approach, which I am excited to explore further, highlights how simple algebraic rules govern both the complex geometry of correlators and the mathematical properties of multivariate hypergeometric functions.
Insights from Scattering Amplitudes. The true mathematical beauty of flat-space scattering amplitudes becomes clear when they are reinterpreted in auxiliary or dual spaces. For instance, exploring how causal dynamics is embedded in these amplitudes led to the discovery of new geometric structures like the amplituhedron. This structure generalises familiar shapes like triangles and polygons to higher-dimensional spaces. At the same time, scattering amplitudes admit Feynman integral representations, raising an intriguing question: what kinds of mathematical functions do these integrals generate? In flat space, loop integrals produce certain classes of iterated integrals and elliptic functions, with possible further generalisations. In cosmology, even the simplest tree-level correlators lead to more complex functions, such as polylogarithms and generalised hypergeometric functions.
One of the questions I'm interested in is: Can we formally study these function classes based on the properties of correlators? And conversely, can we learn something useful about correlators by studying the structures and behaviours of these functions? There are two related approaches to tackling this problem: the geometrical and dynamical perspectives.
Focusing solely on kinematics, the geometrical approach recognises that simple correlators can be seen as the canonical forms of a polytope, whose positive geometry makes properties such as locality and unitarity emergent. On the other hand, the dynamical approach examines the kinematic differential equations that these correlators satisfy. This growing field of research is revealing exciting connections between cosmological correlators and mathematical areas like twisted cohomology.
Rather than studying correlators directly in kinematic space, reformulating them in Mellin space transforms the problem into one of analysing higher-fold Mellin-Barnes integrals, whose solutions depend on triangulating a set of points. Different triangulations lead to various relationships between correlators, such as Euler's reflection identities. This approach, which I am excited to explore further, highlights how simple algebraic rules govern both the complex geometry of correlators and the mathematical properties of multivariate hypergeometric functions.
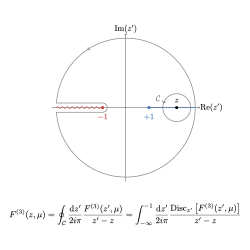
 Off-Shell Methods. The development of off-shell methods for scattering amplitudes is deeply tied to the power of complex analysis. This approach has its roots in the famous Kramers-Kronig relations, which established the key link between causality and analyticity. Building on this, the complex deformation of momenta has led to major advances, such as the Berends-Giele recursion relations, and a clearer understanding of the analytic structure of the S-matrix.
Rethinking kinematic constraints and symmetries has revealed the mathematical beauty hidden in scattering amplitudes. These new methods not only enhance our understanding of quantum field theory but also make it easier to compute complex physical processes, as demonstrated by recent progress in high-loop calculations. In cosmology, however, such advanced techniques are still in their infancy, and pushing the boundaries of computational methods is a challenging task. To address this, I recently proposed a systematic off-shell study of cosmological correlators. This approach not only clarifies the origin of correlator singularities and factorisation but also makes analytical computations more manageable.
This opens up exciting new possibilities for sewing together simple building blocks to construct more complex correlators, with the potential to develop cosmological recursion relations in the future.
Off-Shell Methods. The development of off-shell methods for scattering amplitudes is deeply tied to the power of complex analysis. This approach has its roots in the famous Kramers-Kronig relations, which established the key link between causality and analyticity. Building on this, the complex deformation of momenta has led to major advances, such as the Berends-Giele recursion relations, and a clearer understanding of the analytic structure of the S-matrix.
Rethinking kinematic constraints and symmetries has revealed the mathematical beauty hidden in scattering amplitudes. These new methods not only enhance our understanding of quantum field theory but also make it easier to compute complex physical processes, as demonstrated by recent progress in high-loop calculations. In cosmology, however, such advanced techniques are still in their infancy, and pushing the boundaries of computational methods is a challenging task. To address this, I recently proposed a systematic off-shell study of cosmological correlators. This approach not only clarifies the origin of correlator singularities and factorisation but also makes analytical computations more manageable.
This opens up exciting new possibilities for sewing together simple building blocks to construct more complex correlators, with the potential to develop cosmological recursion relations in the future.
 Non-Perturbative Numerical Bootstrap. Conformal field theories (CFTs) are unique because they look the same at all scales and energies, which makes them both hard to understand intuitively (for example using dimensional analysis) and among the simplest theories in physics. They are crucial for understanding critical points in phase transitions and are central to the study of quantum field theories (QFTs), as they lie at fixed points of renormalization group flows, from which many QFTs emerge.
Studying and classifying CFTs is a key goal in modern theoretical physics, and they are also incredibly important in cosmology for several reasons. First, new physics in the early Universe, possibly a strongly coupled CFT, could have left imprints in the sky by weakly coupling to the observed fluctuations. Second, the symmetries of de Sitter space, which approximately describe the Universe during inflation, become conformal symmetries on the late-time boundary. This means that spatial correlation functions should follow (approximate) conformal rules. While we already know the two-point function is (nearly) scale-invariant, more complex correlations still need to be observed. Finally, if we could constrain these cosmological correlations directly in real space, we could use map-level inference techniques to detect primordial signals in the sky, free of late-time non-linearities.
A powerful strategy behind studying and solving strongly coupled CFTs is to combine conformal invariance (infinite correlation length) with the existence of the operator product expansion. This is known as conformal bootstrap, it heavily employs sophisticated numerical algorithms. Essentially, one uses crossing relations as consistency conditions to winnow down the range of CFT data (scaling dimensions and a finite set of free numerical parameters). In practice, this boils down to solve a set of highly non-trivial recurrence relations or infinite number of constraints to find the functional dependence of conformal blocks. Several very sophisticated techniques, like convex optimization and semidefinite programming, have been developed to tackle these problems, resulting in bounds and allowed regions for CFTs as well as getting access to their spectrum.
I aim to apply my strong numerical skills to adapt these cutting-edge methods to the study of high-energy theories of the early Universe.
The potential outcomes for primordial cosmology are significant—not only could this work refine the space of possible inflationary theories, but it could also uncover new signals that have been completely overlooked.
Non-Perturbative Numerical Bootstrap. Conformal field theories (CFTs) are unique because they look the same at all scales and energies, which makes them both hard to understand intuitively (for example using dimensional analysis) and among the simplest theories in physics. They are crucial for understanding critical points in phase transitions and are central to the study of quantum field theories (QFTs), as they lie at fixed points of renormalization group flows, from which many QFTs emerge.
Studying and classifying CFTs is a key goal in modern theoretical physics, and they are also incredibly important in cosmology for several reasons. First, new physics in the early Universe, possibly a strongly coupled CFT, could have left imprints in the sky by weakly coupling to the observed fluctuations. Second, the symmetries of de Sitter space, which approximately describe the Universe during inflation, become conformal symmetries on the late-time boundary. This means that spatial correlation functions should follow (approximate) conformal rules. While we already know the two-point function is (nearly) scale-invariant, more complex correlations still need to be observed. Finally, if we could constrain these cosmological correlations directly in real space, we could use map-level inference techniques to detect primordial signals in the sky, free of late-time non-linearities.
A powerful strategy behind studying and solving strongly coupled CFTs is to combine conformal invariance (infinite correlation length) with the existence of the operator product expansion. This is known as conformal bootstrap, it heavily employs sophisticated numerical algorithms. Essentially, one uses crossing relations as consistency conditions to winnow down the range of CFT data (scaling dimensions and a finite set of free numerical parameters). In practice, this boils down to solve a set of highly non-trivial recurrence relations or infinite number of constraints to find the functional dependence of conformal blocks. Several very sophisticated techniques, like convex optimization and semidefinite programming, have been developed to tackle these problems, resulting in bounds and allowed regions for CFTs as well as getting access to their spectrum.
I aim to apply my strong numerical skills to adapt these cutting-edge methods to the study of high-energy theories of the early Universe.
The potential outcomes for primordial cosmology are significant—not only could this work refine the space of possible inflationary theories, but it could also uncover new signals that have been completely overlooked.
For more details, see [Spectral Representation Paper]
Effective Field Theory Techniques
Bridging scales: the UV/IR connection (for aficionados and experts)
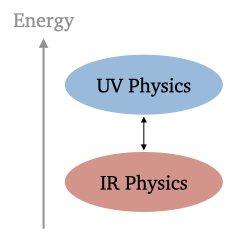 EFT Philosophy. Nature operates on many different length scales. Fortunately, when studying a particular physical phenomenon, we don’t need to know what’s happening at every scale at once. In fact, the macroscopic behaviour at one scale can usually be described without the full details of the microscopic scales, as long as there’s a large enough separation of scales between them. This is the core idea behind Effective Field Theory (EFT)! In systems where there is a clear separation of scales, the influence of small-scale physics on large-scale dynamics tends to "decouple", meaning its effects are small and come with corrections that get smaller as the scale difference increases. The practical use of EFTs is that these corrections can be systematically organised and controlled, making the theory predictive and allowing us to calculate observables to a desired level of accuracy. There are two main approaches to EFTs: top-down and bottom-up. The top-down approach starts from a known high-energy theory (UV) and simplifies it by "integrating out" the physics above a certain energy scale. This approach is useful when for example the UV physics is non-perturbative and we only need to describe the light degrees of freedom. Although this method generates an infinite series of corrections, they can usually be safely ignored beyond a certain precision. However, the real power of EFT comes from the bottom-up approach, especially when the UV theory is unknown. Here, we construct the low-energy theory (IR) by incorporating only the relevant degrees of freedom and respecting key symmetries. The unknown parameters in this approach are determined by experiments or, in cosmology, by observations. While the EFT philosophy might seem straightforward, applying it in a mathematically consistent way reveals some of the most fascinating and elegant aspects of physics.
EFT Philosophy. Nature operates on many different length scales. Fortunately, when studying a particular physical phenomenon, we don’t need to know what’s happening at every scale at once. In fact, the macroscopic behaviour at one scale can usually be described without the full details of the microscopic scales, as long as there’s a large enough separation of scales between them. This is the core idea behind Effective Field Theory (EFT)! In systems where there is a clear separation of scales, the influence of small-scale physics on large-scale dynamics tends to "decouple", meaning its effects are small and come with corrections that get smaller as the scale difference increases. The practical use of EFTs is that these corrections can be systematically organised and controlled, making the theory predictive and allowing us to calculate observables to a desired level of accuracy. There are two main approaches to EFTs: top-down and bottom-up. The top-down approach starts from a known high-energy theory (UV) and simplifies it by "integrating out" the physics above a certain energy scale. This approach is useful when for example the UV physics is non-perturbative and we only need to describe the light degrees of freedom. Although this method generates an infinite series of corrections, they can usually be safely ignored beyond a certain precision. However, the real power of EFT comes from the bottom-up approach, especially when the UV theory is unknown. Here, we construct the low-energy theory (IR) by incorporating only the relevant degrees of freedom and respecting key symmetries. The unknown parameters in this approach are determined by experiments or, in cosmology, by observations. While the EFT philosophy might seem straightforward, applying it in a mathematically consistent way reveals some of the most fascinating and elegant aspects of physics.
 EFT for Primordial Fluctuations. In primordial cosmology, how can we construct theories that describe the early Universe's fluctuations without relying on the unknown microscopic details of high-energy physics? The solution lies in using the EFT approach! The first step is to identify the relevant degree of freedom. During inflation, the inflationary background spontaneously breaks time-translation symmetry, so the key field describing these fluctuations is the corresponding Goldstone boson. This field is actually directly connected to the observable adiabatic fluctuations we see in the sky. With this in mind, we can then write the most general action possible that respects the symmetries of the system. At every order, the terms in the action are fixed by spatial diffeomorphism invariance, with only a finite number of free coefficients. This general framework includes general relativity but is much broader as it is less constrained. This EFT provides a unified description of many different particular models, enables us to derive general predictions such as equilateral non-Gaussianities, and allows for neat extensions in a controlled manner. However, we have clearly only scratched the surface of a large and fascinating subject. Recent advancements have focused on connecting EFT interactions, and in particular Wilson coefficients, to specific UV theories at the background level. Explicit inflationary model dynamics have been mapped to the fluctuations and time-varying couplings. This has been used to study features during inflation—subtle signals hidden in the running of cosmological correlators. Beyond the observable Goldstone boson, other degrees of freedom covering the entire mass spectrum are generically expected to be present in the early Universe. This raises the question of how to expand simple theories to include these additional particles. Recently, I worked on connecting spinning fields with a helical chemical potential to observable phenomena, which expanded the EFT of inflationary fluctuations and uncovered new parity-violating signals. A current open question is how to incorporate fermions into this framework. To do this, we need to introduce vielbeins to describe spinors in three-dimensional space and then perform a time diffeomorphism to create a four-dimensional structure that is compatible with the symmetries. This will be my next goal.
EFT for Primordial Fluctuations. In primordial cosmology, how can we construct theories that describe the early Universe's fluctuations without relying on the unknown microscopic details of high-energy physics? The solution lies in using the EFT approach! The first step is to identify the relevant degree of freedom. During inflation, the inflationary background spontaneously breaks time-translation symmetry, so the key field describing these fluctuations is the corresponding Goldstone boson. This field is actually directly connected to the observable adiabatic fluctuations we see in the sky. With this in mind, we can then write the most general action possible that respects the symmetries of the system. At every order, the terms in the action are fixed by spatial diffeomorphism invariance, with only a finite number of free coefficients. This general framework includes general relativity but is much broader as it is less constrained. This EFT provides a unified description of many different particular models, enables us to derive general predictions such as equilateral non-Gaussianities, and allows for neat extensions in a controlled manner. However, we have clearly only scratched the surface of a large and fascinating subject. Recent advancements have focused on connecting EFT interactions, and in particular Wilson coefficients, to specific UV theories at the background level. Explicit inflationary model dynamics have been mapped to the fluctuations and time-varying couplings. This has been used to study features during inflation—subtle signals hidden in the running of cosmological correlators. Beyond the observable Goldstone boson, other degrees of freedom covering the entire mass spectrum are generically expected to be present in the early Universe. This raises the question of how to expand simple theories to include these additional particles. Recently, I worked on connecting spinning fields with a helical chemical potential to observable phenomena, which expanded the EFT of inflationary fluctuations and uncovered new parity-violating signals. A current open question is how to incorporate fermions into this framework. To do this, we need to introduce vielbeins to describe spinors in three-dimensional space and then perform a time diffeomorphism to create a four-dimensional structure that is compatible with the symmetries. This will be my next goal.
Perturbativity Bounds. It is important to ensure that the effective description of fluctuations presented above is under theoretical control and identify the natural hierarchy of scales of the system. Since the theory contains non-renormalisable interactions, it will become strongly coupled at a certain energy scale. In this context, I contributed to deriving the full set of perturbativity bounds for a widely studied theory where an additional massive scalar field is coupled to the adiabatic sector, both in weak and strong mixing scenarios. These bounds can be determined either by finding the highest energy at which the tree-level scattering remains unitary or by identifying the strong coupling scales through power counting. Notably, I demonstrated the existence of a large physical regime where strong mixing occurs without leading to strong coupling, opening up a range of phenomenologically interesting and previously overlooked signals. Another important aspect of a healthy EFT is naturalness. In simple terms, quantum corrections tend to push particle masses toward the scale of the heavy physics that has been integrated out, making the theory radiatively unstable. This issue is less understood in the context of the early Universe, as it involves complex calculations of loop diagrams.
Non-local EFT. Integrating out heavy degrees of freedom leads to non-local interactions in time and space. Loosely speaking, locality is related to the effects of a field decreasing with distance, which shows up as inverse gradients in the action. However, something remarkable happens when the light particle has a reduced speed of sound. Such non-relativistic dispersion relation implies that the momentum dominates over the energy of the particle, and the non-locality becomes effectively local in time, but the effective theory still remains non-local in space. For the purists, this approximation corresponds to replacing the Feynman propagator with a Yukawa-type potential. I have recently shown that such non-local EFT is extremely handy for making predictions. It has three main advantages: (i) it has a single simple degree of freedom, (ii) it accurately captures the effects of high-energy physics, and (iii) corrections can be systematically computed. However, such EFT has been derived from a given UV theory, following a top-down approach. It would be interesting from a theoretical perspective to investigate the possibility of systematically constructing a set of boost-breaking EFTs that are non-local in space, yet still consistent with a local UV completion. This would enables us derive simple correlators than might reveal new signatures of some UV physics that we've missed.
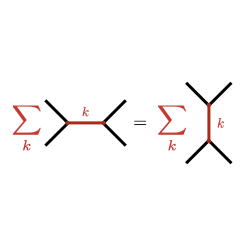
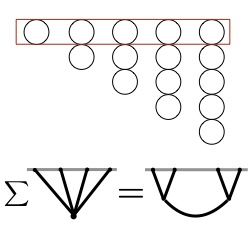 Resummation Techniques. When computing cosmological observables, we face the problem that exact answers are out of reach. So, we have two options: either give up or do what physicists usually do—use perturbation theory. Instead of trying to compute the entire probability distribution of primordial fluctuations, we focus on the first few cumulants because they are easier to handle. Similarly, when working with cosmological correlators, it's much simpler to compute contact diagrams than exchange diagrams. But this raises an interesting question: can we recover some of the missing complexity by only computing the simpler parts? In other words, how much of the high-energy details (what has been integrated out) can we reconstruct from the low-energy ones (which are easier to compute)?
In the context of cosmological correlators, this means: can we reconstruct exchange diagrams by adding up contact ones? While this is straightforward for flat-space scattering amplitudes, in cosmology, things get much more complicated. In fact, the series we obtain are divergent. This isn't surprising since we expect non-perturbative effects to kick in, such as spontaneous particle production. It’s similar to how, in QED, summing Feynman diagrams diverges after around the 137th order (the inverse of the fine-structure constant, which isn’t a coincidence!). To make meaningful predictions, we need more advanced techniques, such as the Borel method, to resum these asymptotic series.
For particle propagation in the early Universe, this is like solving the Kadanoff-Baym equation to capture the full non-perturbative behaviour. Ideally, the ultimate goal would be to resum correlators to obtain non-perturbative predictions for the wavefunction of the Universe itself—the probability distribution of a fluctuation field configuration at the end of inflation. It’s possible that the new physics we're searching for is strongly coupled but only weakly interacts with the visible sector. In simpler terms, what’s the cosmological collider equivalent of non-perturbative jets and hadronic physics from particle colliders?
Exploring this research direction will lead us into the fascinating world of resurgence theory, which I plan to investigate further in the future.
Resummation Techniques. When computing cosmological observables, we face the problem that exact answers are out of reach. So, we have two options: either give up or do what physicists usually do—use perturbation theory. Instead of trying to compute the entire probability distribution of primordial fluctuations, we focus on the first few cumulants because they are easier to handle. Similarly, when working with cosmological correlators, it's much simpler to compute contact diagrams than exchange diagrams. But this raises an interesting question: can we recover some of the missing complexity by only computing the simpler parts? In other words, how much of the high-energy details (what has been integrated out) can we reconstruct from the low-energy ones (which are easier to compute)?
In the context of cosmological correlators, this means: can we reconstruct exchange diagrams by adding up contact ones? While this is straightforward for flat-space scattering amplitudes, in cosmology, things get much more complicated. In fact, the series we obtain are divergent. This isn't surprising since we expect non-perturbative effects to kick in, such as spontaneous particle production. It’s similar to how, in QED, summing Feynman diagrams diverges after around the 137th order (the inverse of the fine-structure constant, which isn’t a coincidence!). To make meaningful predictions, we need more advanced techniques, such as the Borel method, to resum these asymptotic series.
For particle propagation in the early Universe, this is like solving the Kadanoff-Baym equation to capture the full non-perturbative behaviour. Ideally, the ultimate goal would be to resum correlators to obtain non-perturbative predictions for the wavefunction of the Universe itself—the probability distribution of a fluctuation field configuration at the end of inflation. It’s possible that the new physics we're searching for is strongly coupled but only weakly interacts with the visible sector. In simpler terms, what’s the cosmological collider equivalent of non-perturbative jets and hadronic physics from particle colliders?
Exploring this research direction will lead us into the fascinating world of resurgence theory, which I plan to investigate further in the future.
Positivity. To construct low-energy theories, we need to include all possible operators that are consistent with the symmetries of the system. In doing so, the effects of UV physics are encoded in the coefficients of these operators. But these coefficients aren't completely free! Certain properties of the UV, like Lorentz invariance, locality, and unitarity, impose constraints on them. These constraints are known as positivity bounds. There are various ways to derive these bounds, such as studying causal properties of two-to-two scattering processes or using the analytic properties of Green's functions for conserved quantities.
However, translating these bounds directly into early Universe theories isn’t straightforward. First, the existence of a preferred frame in cosmology breaks Lorentz invariance, which is a key feature of flat-space physics. Second, these bounds usually rely on the behaviour of low-energy particles, which aren't well-defined at very high energies. They only apply in the sub-Hubble regime, where the space-time curvature is small, and gravity is weak.
Recent progress has shown that we can impose such bounds if the UV theory is conformal, but this is generally not true for inflationary cosmology. This means we need a new approach and new mathematical tools that can carry over the useful properties of flat-space scattering amplitudes to cosmological settings. Ultimately, this could help us narrow down the possible theories of inflation.
In practice, this opens the door to a "cosmological numerical bootstrap" program, inspired by the successful S-matrix bootstrap, and I plan to apply my numerical skills to explore this exciting direction.
In the end, I believe that the success of deriving robust and precise preditions for cosmological observables heavily relies on our ability to construct complete and theoretically motivated theories of the early Universe. There's still plenty of exciting physics to explore!
For more details, see [Perturbativity Bounds & Naturalness Paper]
[Non-local EFT Paper]
Other Interests
Below is a non-exhaustive list of topics I am also interested in
 Late-time Universe. Understanding how theoretical predictions of the early Universe can be practically extracted from concrete late-time observational data is important for an early Universe theoretical physicist like me. I am for example interested in the design and use of appropriate estimators to extract signals from the LSS or the CMB data. I am also interested in simulations of the non-linear late-time Universe on small scales. This involves providing the theoretical data for initialising N-body simulations that fully encode non-linear phenomena at play during cosmic structure formation, such as baryionic physics. I am also interested in how the physics from these simulations can be extracted and how robust and fast emulators for efficient forward modelling can be constructed.
Late-time Universe. Understanding how theoretical predictions of the early Universe can be practically extracted from concrete late-time observational data is important for an early Universe theoretical physicist like me. I am for example interested in the design and use of appropriate estimators to extract signals from the LSS or the CMB data. I am also interested in simulations of the non-linear late-time Universe on small scales. This involves providing the theoretical data for initialising N-body simulations that fully encode non-linear phenomena at play during cosmic structure formation, such as baryionic physics. I am also interested in how the physics from these simulations can be extracted and how robust and fast emulators for efficient forward modelling can be constructed.
 Dark Era of Inflation. Ironically, the physics of the early Universe has so far only been constraints on large scales, while the physics of the remaining 50 or so efolds of inflation are still a mystery. The reason is simple: traditional observation methods can't reach such small scales. However, with new tools like the future space-based observatory LISA, we will soon be able to study them using gravitational waves! This will allow us to explore new physics, like the possibility of primordial black holes being dark matter, through the stochastic background of gravitational waves. The main challenge will be separating all the different signals—whether from inflation, phase transitions, or cosmic strings—in what will be a noisy mix of overlapping information.
Dark Era of Inflation. Ironically, the physics of the early Universe has so far only been constraints on large scales, while the physics of the remaining 50 or so efolds of inflation are still a mystery. The reason is simple: traditional observation methods can't reach such small scales. However, with new tools like the future space-based observatory LISA, we will soon be able to study them using gravitational waves! This will allow us to explore new physics, like the possibility of primordial black holes being dark matter, through the stochastic background of gravitational waves. The main challenge will be separating all the different signals—whether from inflation, phase transitions, or cosmic strings—in what will be a noisy mix of overlapping information.
Machine Learning Techniques. Learning physics from the sky is challenging because: (i) it gives only limited information (we have basically one sky to look at), (ii) the physics is usually highly non-linear (at least at late time and at small scales), (iii) we are (and will be even more) overwhelmed by large data sets, and finally (iv) these data sets are frequently contaminated by various systematics. To address these challenges, novel automatic, fast, and tremedously performant techniques are becoming widely used by cosmologists. I am broadly interested in new developments in machine learning for this field. This includes using machine learning to classify cosmological data, recognise patterns, solve complex physical optimisation problems, and train efficient and accurate emulators.